研究室の学び
離散最適化のアルゴリズムについて研究をしています。「最適化」とは多くの選択肢の中から一番「よい」ものを求めることで、例えば経路探索や荷物の詰め込みなど、誰もが日常的に行っていることです。離散最適化の研究においては、数学的能力ももちろんですが、証明の文章をきちんと書けるなどといった論理的思考能力やプレゼンス能力が特に重要になります。本研究室では、離散最適化の研究を通じ、これらの能力の育成に特に力を入れています。
社会との接点
皆さん電車で出かける際には、乗換案内ソフトで出発地から目的地への乗換順を検索していると思います。このとき乗換案内ソフトの中では、「最短路問題」という2地点間の最短経路を求める最適化問題が解かれています。
また、セールスマンが、事務所を出発して顧客の家をすべて回り、また事務所へ戻ってくる最短の経路を知りたいという場合もあるでしょう。こちらは、「巡回セールスマン問題」とよばれるやはり代表的な最適化問題です。
このように、最適化問題は日常の中に自然に現れ、誰もが無意識に解いている問題です。本研究室では、特に離散最適化問題に対する効率的な解法設計の研究をしています。
実は、上記の最短路問題と巡回セールスマン問題はよく似た問題ですが、その難しさは大きく異なり、最短路問題は簡単に解け、巡回セールスマン問題に対する効率的な解法は現在知られていません。このような問題に対して、理論的あるいは現実的な解法の模索や、問題の解きやすさに繋がる構造の解析を、数理的な視点から行っています。
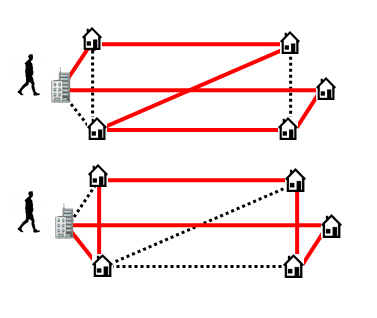
巡回セールスマン問題の解、下の解が最適解
主な研究テーマ
- クラスター巡回セールスマン問題に対する近似率の改善
- 最大利益郵便配達人問題に対する発見的アルゴリズム
- 整数最適化を用いたブンデスリーガの残留ラインに関する通説の検証
- その他,離散最適化の理論や応用についての研究
© Hosei University



